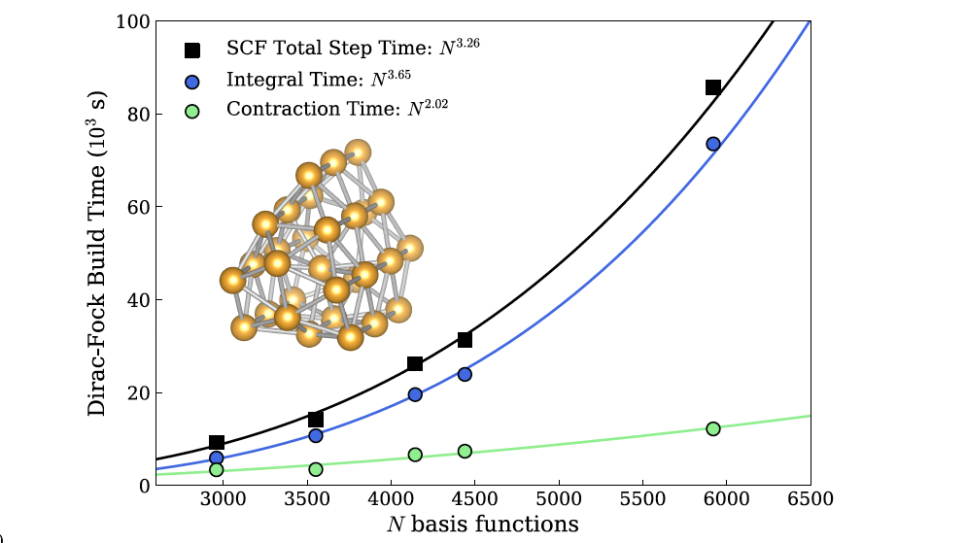
24-core parallel performance of the new 4c Dirac-Hartree-Fock algorithm with the Dirac-Coulomb operator. A series of Au clusters (Au20 to Au40) were used for this test. The computational cost for the densityintegral contraction step has been drastically reduced to the theoretical limit with the Pauli quaternion representation.